엑셀 AZURE 머신러닝 시계열 데이터 분석 방법
엑셀 머신러닝 시계열 분석 기법 목차 바로가기
영상강의
예제파일 다운로드
오빠두엑셀의 강의 예제파일은 여러분을 위해 자유롭게 제공하고 있습니다.
- [엑셀고급] 엑셀 머신러닝 시계열데이터 분석예제파일[엑셀고급] 엑셀 머신러닝 시계열데이터 분석완성파일
중요 알림 : 24년 8월부터 기존의 Azure 머신러닝 스튜디오가 새로운 UI로 모두 개편됨에 따라,
영상에서 다룬 기능은 24년 8월 이후부터는 사용할 수 없습니다.
엑셀 Azrue 머신러닝 다운로드 링크
- Azure Machine Learning 홈페이지 :
https://studio.azureml.net/ - Auto.Arima 모델 데이터 분석 머신러닝 다운로드 :
https://gallery.azure.ai/Experiment/e7fb463caa22454a84286668cfec533f
엑셀 회귀분석 기초
데이터 분석에는 다양한 종류와 기법이 사용됩니다. 그 중 가장 보편적으로 사용되는 데이터분석 기법으로는 '회귀분석'과 '시계열분석'이 있습니다.
그 중 변수가 하나인 회귀분석은 엑셀의 간단한 차트와 함수만으로 아주 손쉽게 해결할 수 있습니다. 예를들어 광고노출수에 대한 매출 변화량, 직원수 증가에 대한 업무효율성 변화량 등 하나의 변수에 대한 분석을 아주 손쉽게 진행할 수 있는데요.
시계열분석을 본격적으로 알아보기 전에, 클릭 몇 번만으로 손쉽게 진행가능한 회귀분석에 대해서 우선 알아보겠습니다.
회귀분석(Regression Analysis)이란 ‘관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한뒤 적합도를 측정해 내는 분석 방법’입니다. 쉽게 말해서, 어떤 조건이 변할 때 나타나는 결과를 보고 조건과 결과의 관계성을 구하는 방법입니다. 수학적으로는 그래프의 x(가로축)과 y(세로축)의 다항식을 구하는 과정이라고 볼 수 있습니다.
그렇다면 ‘다중회귀분석’은 무엇일까요? 말그대로 변수가 여러 개 있을 때의 조건-결과간의 관계성을 구하는 과정이라고 이해하시면 되겠습니다.
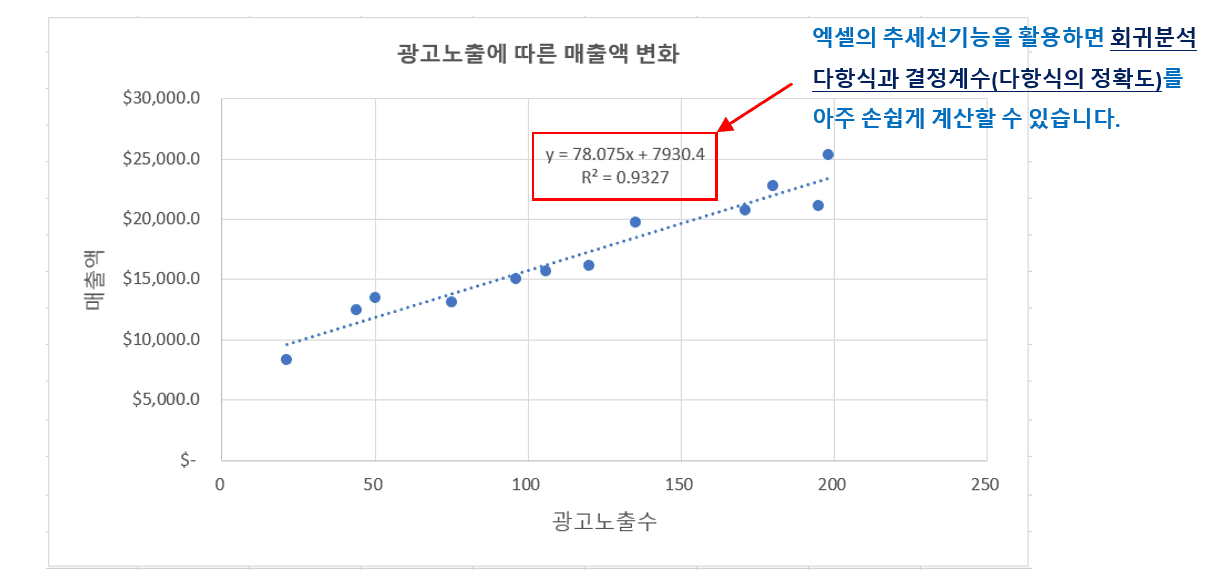
엑셀의 차트와 추세선기능을 활용하면 선형회귀분석 다항식과 결정계수가 자동으로 계산하여 출력할 수 있습니다. 엑셀 차트의 추세선기능과 FORECAST 함수를 사용하면 엑셀이 자동으로 선형회귀분석을 한 뒤 x 변수에 따른 y 결과값을 예측합니다. 차트의 추세선 기능을 활용하는 방법은 영상강의에서 자세히 설명해드렸습니다.
FORECAST 함수의 사용법은 아래 관련 포스트에서 확인할 수 있습니다.
엑셀 시계열분석 - 단순이동평균 예측 기법
시계열 데이터 분석은 더욱 간단합니다. 단어의 뜻 그대로 '시간의 흐름에 따른 데이터를 분석하고 미래의 값을 예측' 하는 데이터분석 기법인데요. 그래프로 본다면 x축(가로축)이 ‘시간의 흐름’이 되고, y축(세로축)이 값의 변화로 출력되는 모양이 되겠습니다.
평소에 많이 사용되는 '연도별 인구 통계', '일별 매출현황' 등 시간의 흐름에 관련된 데이터라면 시계열분석으로 미래의 값을 예측할 수 있습니다.
그렇다면 회귀분석과 시계열분석의 차이점은 무엇일까요?
시계열분석은 자기상관성(correlation)을 전제로 데이터를 분석합니다. 즉, ‘이전시간에 있던 데이터가 이후시간의 데이터에 영향을 주고있어!’라는 것을 전제로 데이터를 분석한다는 것이죠.
이러한 관점에서, 단순이동평균예측(Simple-Moving Average, SMA)은 데이터의 자기상관성을 전제로 하여 이전에 발생한 데이터들의 주기성을 계산 한 뒤, 각 주기마다의 평균을 구해서 미래의 값을 예측하는 기법입니다.
이번 강의에서는 예제파일의 ‘전국 미세먼지 오염도 예측’ 시트를 기준으로 알아볼 예정인데요. 미세먼지 오염도 시트에는 2010년도 1월부터 2018년도 12월까지의 자료가 있습니다. 여기에서 2010년-2016년의 자료를 바탕으로 2017,2018년도 자료를 예측하고 실제 값과 얼마나 차이가 나는지 절대평균오차(MAE, Mean Absolute Error)를 알아보겠습니다.
미세먼지오염도 데이터는 ‘매년’, 즉 ‘12개월을 주기로 값이 변한다.’라고 우리는 이미 알고있습니다. 따라서 2010년부터 2015년 (6년치) 또는 2010년부터 2016년(7년치)의 각 월별 오염도의 단순평균을 계산하여 미래의 값을 예측합니다.
실제 데이터 vs 단순이동평균을 활용하여 예측된 데이터 비교
단순이동평균 계산을 위해 사용한 전체 수식은 예제파일에서 확인하실 수 있습니다. 단순 이동평균을 구하기 위해 사용된 수식
H86셀에 수식을 입력한 뒤, 아래방향으로 자동채우기하면 단순평균 예측이 완료합니다.
=SUM($B2,$B14,$B26,$B38,$B50,$B62)/6
'예제파일 H86셀에 아래 수식을 입력합니다.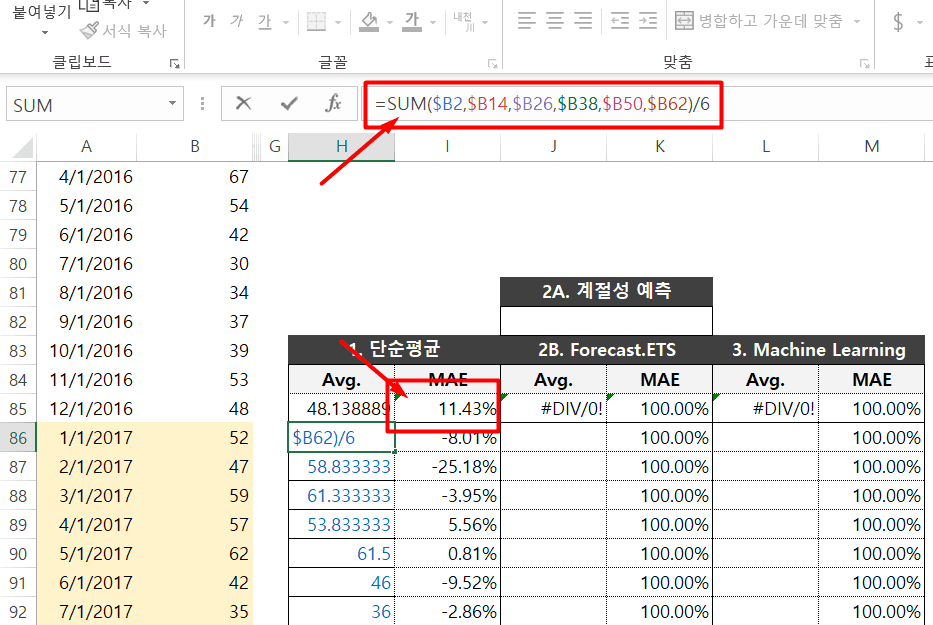
6년치의 값으로 향후 2년 데이터를 단순평균모델로 예측해보니11.5%의 절대평균오차가 나왔습니다. 엑셀 시계열분석 - ETS 모델 예측 기법 (지수평활법)
시계열 데이터의 또 다른 분석 방법으로 ETS(Exponential Smoothing, 지수평활법)모델이 있습니다.
이전 단계에서 알아본 '단순 이동평균 예측 기법'은 과거의 모든 데이터에 동일한 중요도를 부여합니다. 하지만 여기에는 큰 문제가 발생하는데요. 바로, 대부분의 시계열 데이터는 최근에 발생한 데이터가 예전에 발생한 보다 현실을 잘 반영하기 때문에, 중요도가 다르게 설정되어야 한다는 것 입니다.
바로 이 문제점을 보완한 방식이 ETS모델(지수평활법)입니다. ETS 모델은 최근에 발생한 자료일수록 큰 가중치를 부여하여 미래의 값을 예측하는 방법입니다. 미래를 예측한다는 특성상 특정 분석기법이 완벽하다고 정의할 수는 없습니만, ETS모델은 주어진 데이터가 계절성을 가지고 있다면, 어떠한 분석기법 보다도 정확하게 미래의 값을 예측할 수 있다는 장점이 있습니다.
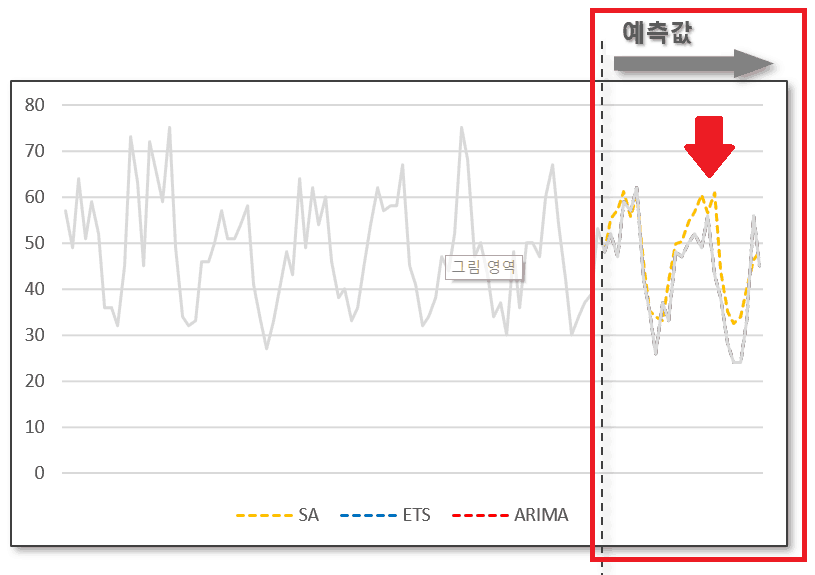
실제 데이터 vs ETS 모델을 활용한 예측 값 비교
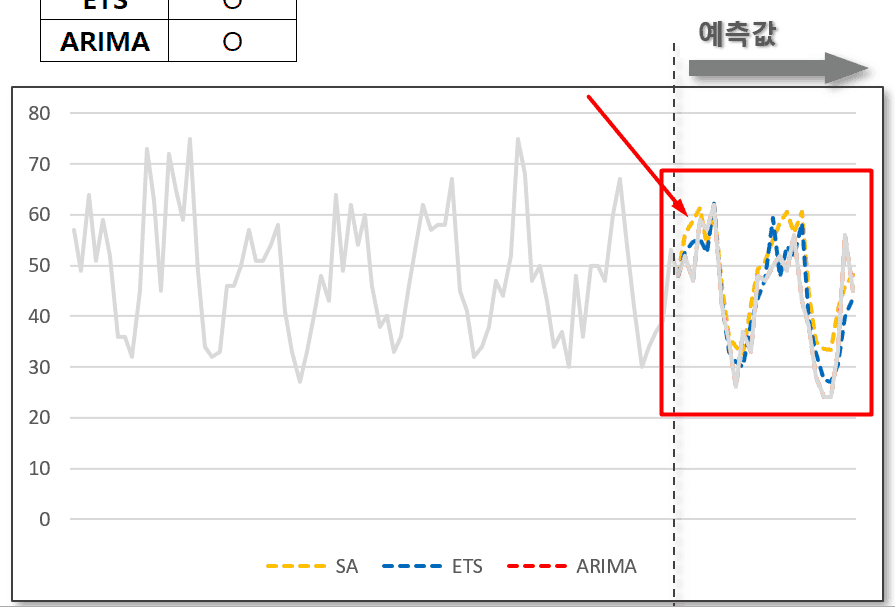
ETS모델(파란색선)을 사용하면 단순평균모델보다 더욱 정확히 미래의 값을 예측할 수 있습니다. 엑셀 FORECAST.ETS 함수 사용하기
엑셀 2016 이후 버전을 사용중이시라면, FORECAST.ETS 함수를 사용하여 ETS 모델 시계열 분석을 아주 손쉽게 적용할 수 있습니다. FORECAST.ETS 함수의 자세한 사용방법은 아래 관련 포스트를 참고하세요.
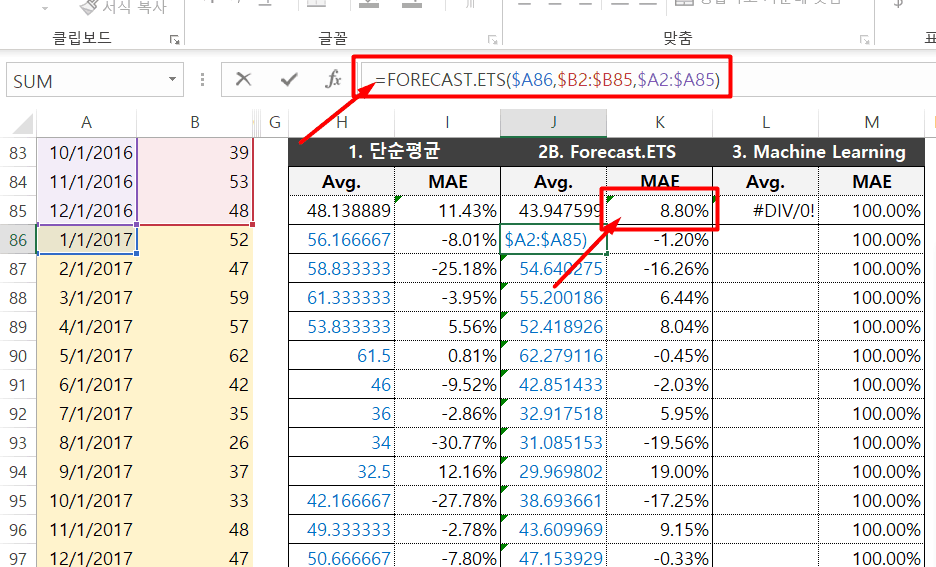
FORECAST.ETS 함수를 사용한 결과, 약 8.8%의 절대평균오차로 향후 2년치의 미세먼지 오염도를 예측하였습니다. 시계열 데이터의 계절성을 분석하는 방법
시계열 데이터를 분석할 때, 또 하나 눈여겨봐야 할 부분은 바로 데이터가 계절성을 띄는지 확인하는 것입니다. 엑셀 2016이후 버전을 사용중이시라면 FORECAST.ETS.SEASONALITY 함수를 사용하여 데이터의 계절성 주기를 손쉽게 계산할 수 있습니다.
FORECAST.ETS.SEASONALITY 함수에 대한 자세한 설명은 아래 관련포스트를 확인해주세요.
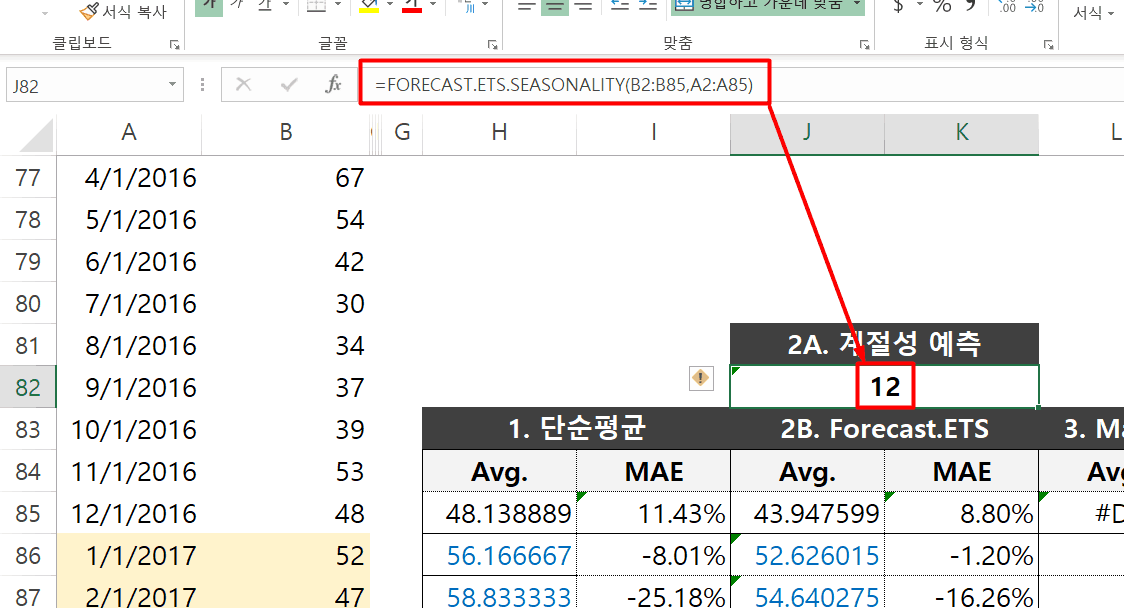
FORECAST.ETS.SEASONALITY 함수를 사용한 결과, 우리가 이미 알고있는것과 같이 12개월의 계절성을 갖는것으로 출력되었습니다. 엑셀 시계열 분석 - Azure 머신러닝 활용
엑셀 2013 이후 버전을 사용 중일 경우, [Office 추가기능]에서 제공하는 Azure Machine Learning을 통하여 더욱 다양하고 고차원적인 데이터 분석이 가능합니다. 이번 강의에서는 엑셀 머신러닝 Arima모델을 기반으로 한 시계열 데이터 예측 기법을 소개합니다.
우선, Arima 모델로 시계열 데이터 분석을 진행하기 전에, ARIMA 모델이란 무엇인지 간단하게 짚고 넘어가겠습니다.
Arima (AutoRegressive Integrated Moving Average) 모델이란, 이전 데이터가 이후 데이터에 영향을 미친다는 ‘자기상관성’에 더해, 데이터가 가지고 있는 추세의 흐름까지 반영하여 데이터를 분석하는 방법입니다. ARIMA 모형에 대한 자세한 설명은 통계학적, 수학적인 부분이 많이 들어가므로 관련서적이나 인터넷자료를 검색하면 다양한 정보가 나와있으니 별도로 확인해보시길 권장드립니다.
이번 강의에서는 학문적인 부분은 최대한 줄이고, ETS 모델과 ARIMA 모델을 실전에서 어떻게 응용하는지 그 방법을 소개해드리고자 합니다.
우선 ARIMA 모델과 ETS모델을 적용하려면, 시계열 데이터의 정상성(Stationarity)와 비정상성(Non-stationrity)에 대해 알아야하는데요. 본론부터 말씀드리면,
#ETS모델은 비정상성데이터에 적합하고, #ARIMA모델은 정상성데이터에 적합합니다.
즉 대부분의 상황에서, 시계열 데이터가
‘계절성’을 강하게 띌 경우 ETS 모델을 사용하는 것이 좋고,
‘자기상관성’을 강하게 띌 경우 ARIMA 모델을 사용하는 것이 좋습니다.정상성 데이터란 ‘시계열(값)의 변동이 시간이 흐름에 따라 일정하게 변하는 데이터’를 말합니다. 다시 말해, 시간이 지나도 분산(데이터의 흩어짐 정도)이 일정한 데이터 집합을 이야기하는데요. 대부분의 실생활에서 나타나는 시계열 데이터는 비정상성 데이터이기 때문에, ARIMA 모델을 제대로 활용하려면 차분을 통해서 비정상성데이터를 정상성데이터로 변환한 뒤에 ARIMA 모델을 적용해야합니다.
즉 ARIMA 모델을 제대로 활용하려면 어느정도 전문적인 통계학적 지식이 필요하다는 것인데요. 그럼에도 불구하고 엑셀 머신러닝을 소개해드리는 이유는, 엑셀 머신러닝을 활용하면 R의 Auto.Arima 함수를 통해 ARIMA 매개변수를 자동으로 계산하고 데이터를 예측분석 할 수 있기 때문입니다.
AZURE 머신러닝 추가기능을 실행한 모습
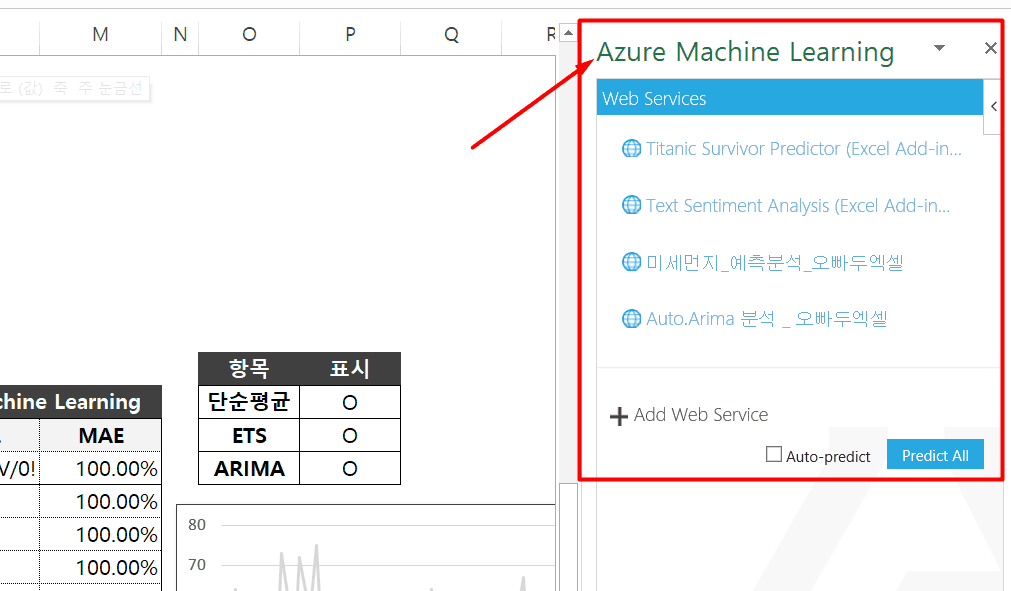
엑셀 2013 이후 버전부터 Azure Machine Learning 추가기능을 사용할 수 있습니다. 엑셀 AZURE 머신러닝으로 시계열 데이터 분석하기
- 엑셀 상단의 [삽입] – [내 추가 기능] – [스토어] 이동한 뒤 ‘Azure’를 검색합니다. 검색 결과에서 ‘Azure Machine Learning’을 선택하여 엑셀에 추가기능을 설치합니다.
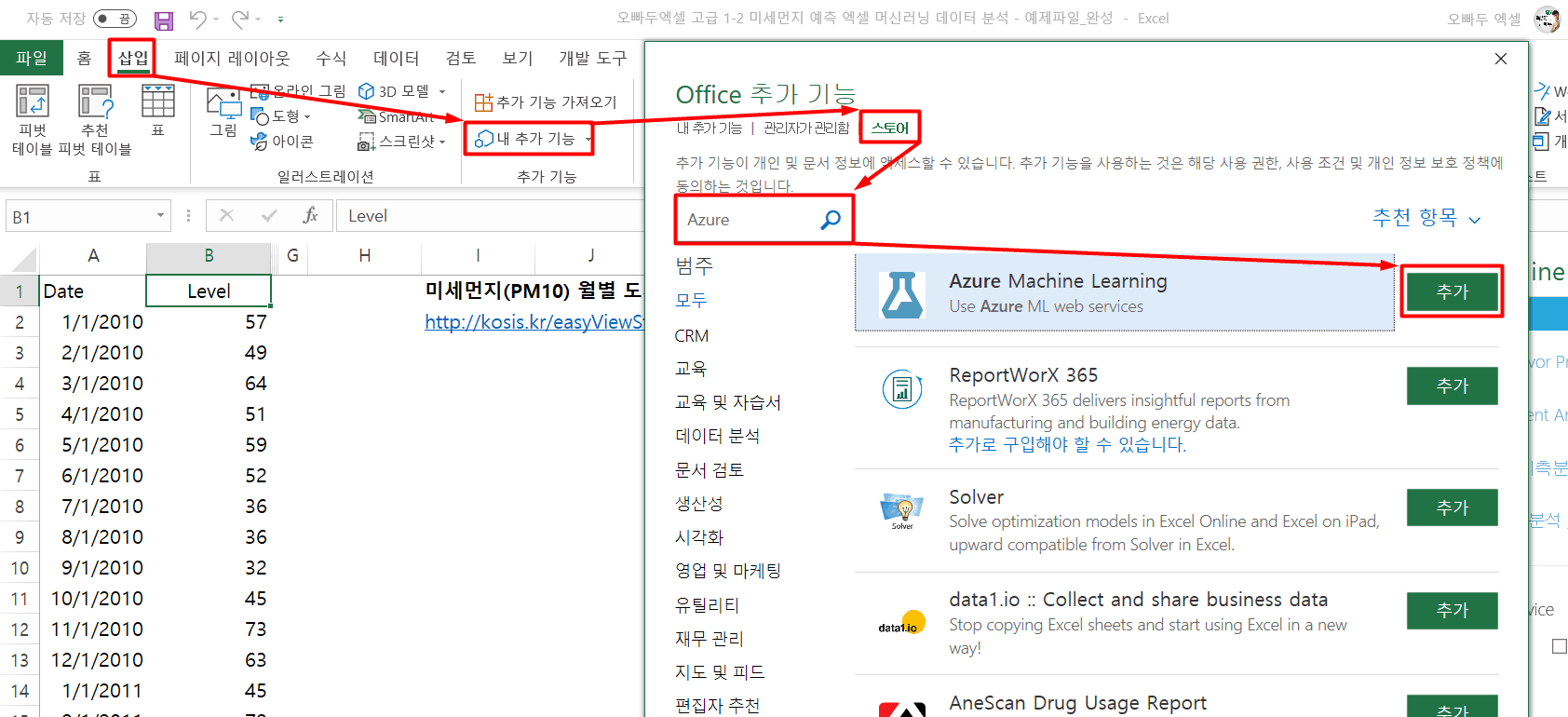
[삽입] – [내추가기능] – [Azure Machine Learning] 추가기능을 엑셀에 추가합니다. - 이후 Azure 머신러닝을 실행하면 우측에 새로운 창이 나타나면서 원하는 Azure 머신러닝 데이터 분석 모델을 저장하여 실행할 수 있습니다. 우측 창에서 ‘+ Add Web Service’ 버튼을 클릭하여 아래의 URL 주소와 API Key 값을 입력합니다.
Add Web Service 버튼을 눌러 분석기법을 추가합니다. 전국 미세먼지 오염도 분석
구분 값 URL 주소 https://ussouthcentral.services.azureml.net/workspaces/31561ac13f3a45ba8c4a97c129c73e93/services/269872e4a2fd4818a65ecd3433a23b65/execute?api-version=2.0&format=swagger API 키 D1AxD1IxEcwB762Gd6MuydaNPCvLOqYJk6slUpKYaKMW0JcSfq7qpzQDUWiPFn02PnUkxE7LDkysjXyUgOqsqQ== Auto Arima 시계열 데이터 분석모델
구분 값 URL 주소 https://ussouthcentral.services.azureml.net/workspaces/31561ac13f3a45ba8c4a97c129c73e93/services/432c1fbabcaa489ba50553fdb1d199fb/execute?api-version=2.0&format=swagger API 키 M5qoD8LTzjnDKeWyHxno/Mrr51z8D7PRVTLOeCOU2NTcC4TuEcyADgZFCyQsEeKnZb2KNq4tQW1gopL8kgU2pw== *주의*
날짜/시간 값이 들어있는 열의 머릿글은 반드시 ‘Date’ 로 입력되어야 합니다. - 적어드린 URL 주소와 API Key 값을 입력하면 아래와 같이 새로운 Azure 엑셀 머신러닝 데이터 분석모델이 추가됩니다.
Azure 엑셀 머신러닝 추가기능에 새로운 데이터 분석모델이 추가되었습니다. - 원하는 데이터 분석 모델을 선택한 뒤, 아래의 순서대로 값을 입력합니다.
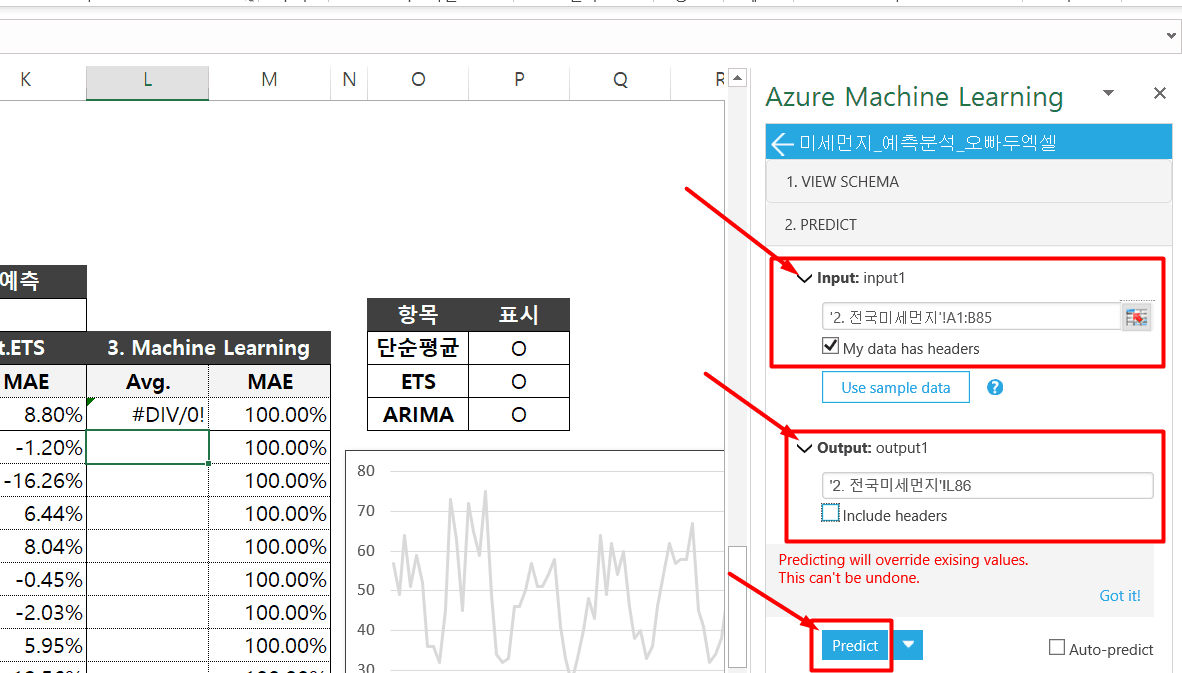 - Input : 데이터 범위를 선택합니다.
- Input : 데이터 범위를 선택합니다.
(주의사항 – 날짜가 입력된 열의 머릿글은 반드시 ‘Date’ 로 입력합니다. 데이터는 [날짜/시간]과 [숫자]로만 이루어진, 총 2개의 열을 가진 데이터범위여야 합니다. 최소 24개 이상의 시계열로 이루어진 데이터에 적용해야만 올바른 예측 값을 출력합니다.)- Output : 예측 값을 출력할 범위의 시작셀을 선택합니다.
(Include Headers – 만약 시작셀 위에 이미 머릿글이 들어가 있는 경우, Include Header 체크박스의 값을 체크해제합니다. )- Predict : Input과 Output을 모두 입력하였으면 Predict 버튼을 눌러 데이터 분석을 시작합니다.
엑셀 시계열 분석 실전예제 - 음료업/식품업 전망 예측
전국 미세먼지 오염도 예측과 동일한 방법으로 음료업/식품업 업황전망 예측에도 시계열 데이터 예측 분석 기법을 적용할 수 있습니다.
- 단순 이동평균 모델
- ETS(지수평활법) 모델
- Auto.ARIMA 모델
위에서 알아본 3가지 데이터 분석기법을 사용하여 향후 2년의 데이터를 예측합니다. 3가지 기법을 활용하여 분석하는 방법은 영상강의에서 자세히 다뤄드렸습니다.
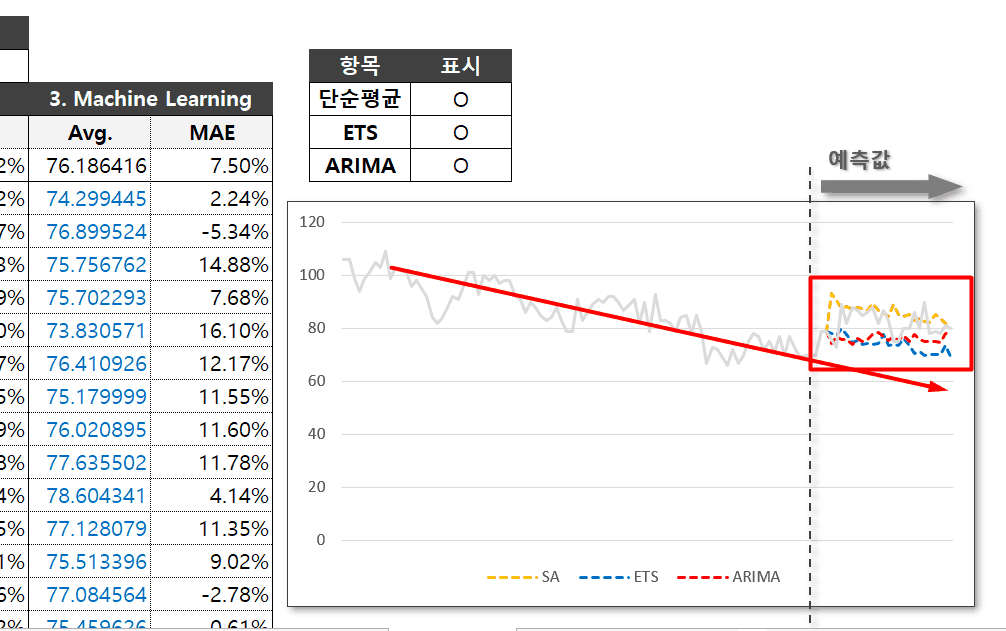
식품업 업황전망의 경우, 기존 데이터를 고려할 시 미래의 데이터가 현상유지 또는 감소할 것으로 예상되었으나, 실생활에서는 예측하기 어려운 다양한 변수가 존재하여 전혀 다른 결과가 나타났습니다. (백종원님의 대단함!) Azure 머신러닝 Auto.Arima 모델 다운로드
Auto.Arima 를 활용한 데이터 분석모델은 아래 링크에서 확인하실 수 있습니다. Microsoft에 회원가입 후, Azure 머신러닝 무료회원으로 가입하면 해당 링크에서 Auto.Arima 모델을 본인의 프로젝트에 바로 다운로드 할 수 있습니다.
(Azure 머신 러닝은 개인회원에게 무료로 제공됩니다!)Azure 머신러닝 홈페이지 바로가기 : https://studio.azureml.net/아래 링크로 이동하면 Auto.Arima 모델을 사용한 Azure Machine Learning 프로젝트를 다운받으실 수 있습니다.

본인의 Azure 머신러닝 프로젝트로 Auto.Arima 데이터 분석모델을 다운로드합니다. 엑셀 머신러닝 시계열분석에 사용된 R 명령문
영상강의에서 잠시 설명드렸던 R코드 명령문을 적어드립니다. 명령문의 각 단계별 동작원리에 대한 자세한 설명은 영상강의를 참고하시거나 관련서적 또는 인터넷 관련 자료를 참고하세요.
R 프로그램 다운로드 링크 : https://ftp.harukasan.org/CRAN/
# 라이브러리 불러오기 library(forecast) library(tseries) # 내문서 폴더의 원하는 파일명 열기 d <- read.csv("파일명") # 데이터의 행 개수 size <- dim(d)[1] # 시작일을 1990날짜 형태로 변환 start <- strptime(as.Date(d$Date[1],origin="1899-12-30"),'%Y-%m-%d') # 시작일의 년/월값 반환 start.year <- as.integer(substr(start,1,4)) start.month <- as.integer(substr(start,6,7)) # 입력된 데이터를 시계열 형태로 변환 ar.ts <- ts(d[1:size,2], frequency=12, start = c(start.year,start.month)) # 데이터를 차트로 출력 plot(ar.ts) # 데이터가 주기성을 띈다는 가정하에, 추세/계절성 분석을 위해 각 항목으로 나누어 차트로 출력 plot(stl(ar.ts, s.window="periodic"))



