엑셀 통계분석의 시작, 대표값 분석의 모든 것 - 핵심정리
엑셀 대표값 분석 목차 바로가기
영상 강의
예제파일 다운로드
오빠두엑셀의 강의 예제파일은 여러분을 위해 자유롭게 제공하고 있습니다.
- [기초레벨업] 엑셀 통계분석의 핵심, 대표값 분석 요약 정리예제파일[기초레벨업] 엑셀 통계분석의 핵심, 대표값 분석 요약 정리완성파일
라이브 강의 전체영상도 함께 확인해보세요!
위캔두 회원이 되시면 매주 오빠두엑셀에서 진행하는 라이브강의 풀영상을 확인하실 수 있습니다.
현업에서 요구하는 통계분석은 "주어진 데이터의 대표값과 통계지표를 올바르게 이해하는 것"에서 부터 시작합니다. 실무에서 사용되는 대표값은 주로 아래 3가지가 사용됩니다.
데이터 목록
1 2 2 3 4 5 25 주요 대표값 3가지
종류 값 설명 평균값(AVERAGE) 6 주어진 데이터 집단의 산술평균(전체합계÷개수)입니다. 중앙값(MEDIAN) 3 데이터를 크기순서대로 나열했을 때 중앙에 위치하는 값입니다. 만약 데이터개수가 짝수일 경우, 중앙에 위치한 두 값의 평균으로 계산합니다. 최빈값(MODE) 2 데이터 집단에서 가장 자주 발생한 값입니다. 위에서 살펴본 대표값과 더불어 실무 통계분석에서 유용하게 사용할 수 있는 통계지표 3가지가 있는데요. 바로 '표준편차'와 '왜도' 그리고 '첨도'입니다. 그 중에서도 표준편차는 데이터가 정규분포를 가진다는 전제 하에서 여러 통계분석에 사용되는 핵심 지표이므로 반드시 숙지하는 것이 좋습니다.
주요 통계지표 3가지
통계지표 설명 표준편차(STDEV) 데이터 분포가 평균으로부터 얼마나 떨어져있는지를 나타내는 지표입니다. 데이터 집단이 정규분포를 가질 경우, 평균으로부터 2x표준편차 떨어진 범위 안에 95%의 데이터가 포함됩니다. 왜도(SKEW) 데이터 분포가 얼마나 좌/우로 기울어져있는지 나타내는 지표입니다. 양수일 경우 왼쪽, 음수일 경우 오른쪽으로 기울어집니다. 일반적으로 -2~2 사이일 경우 정규분포를 갖는다고 이야기합니다. 첨도(KURT) 데이터 분포가 얼마나 뾰족한 형태로 이루어졌는지 나타내는 지표입니다. 값이 클수록 더욱 뾰족한 형태로 분포하게 됩니다. 일반적으로 8보다 작을 경우 정규분포를 갖는다고 이야기합니다. 표준편차는 값(변량)들이 퍼져있는 정도를 나타내는 통계지표입니다. 즉 표준편차가 크면, 값들이 평균으로부터 멀리 떨어져 있거나 들쭉날쭉 불안정하게 분포됩니다.
표준편차를 구하는 순서는 아래와 같습니다. 예를 들어, 아래 5명 학생 시험성적의 표준편차를 계산하겠습니다.
항목 학생1 학생2 학생3 학생4 학생5 값(변량) 77 79 81 83 85 평균 (77+79+81+83+85)÷5 = 81 편차
(변량-평균)77-81 = -4 79-81 = -2 81-81 = 0 83-81 = 2 85-81 = 4 편차제곱 16 4 0 4 16 분산
(편차제곱의 평균)(16+4+0+4+16)÷5 = 8 표준편차 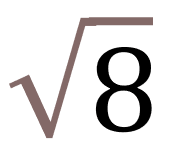 = 2.828427...
= 2.828427...표준편차는 엑셀의 STDEV 함수로 손쉽게 계산할 수 있습니다. 엑셀에 STDEV 함수를 입력하면 STDEV.P 함수와 STDEV.S 함수가 나오는데 P는 Population(모집단)의 약자, S는 Sample(표본집단)의 약자입니다.

함수로 STDEV를 입력하면 STDEV.S와 STDEV.P 함수가 나옵니다. 실무에서는 대부분 샘플링 된 데이터(표본집단)을 다루므로, 특별한 상황을 제외하면 STDEV.S 함수를 사용하는 것이 일반적입니다.
오빠두Tip : 엑셀 2007 이전 버전에서는 STDEV함수 (=STDEV.S)와 STDEVP(=STDEV.P) 함수를 사용합니다.이렇게 계산한 표준편차는 실무에서 어떻게 사용될까요?
현업에서 다루는 대부분의 데이터는 집단의 일부분만 샘플링하게됩니다. 그리고 이렇게 분석된 데이터를 바탕으로 모든 집단을 설명할 수 있는 결과를 제시하게 되는데요.
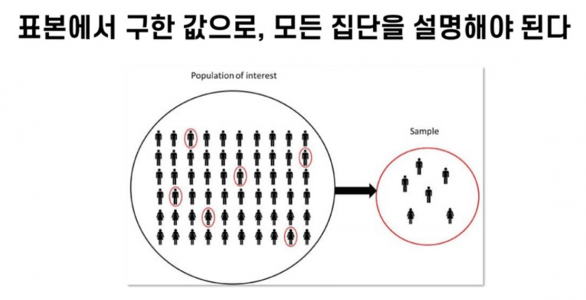
실무에서 다루는 대부분의 데이터는 샘플링된 데이터로 모든 집단을 설명해야 합니다. 이럴 경우, 선택된 표본이 집단의 모든 값을 대표할 수 있다는 가설을 세우기 위해, 데이터 집단이 '정규분포를 따른다' 라는 가정하에 데이터 분석을 진행하게 됩니다. 그리고 데이터 집단이 정규분포를 가질경우, 집단의 95% 데이터는 평균으로부터 2x표준편차가 떨어진 범위안에 포함됩니다.
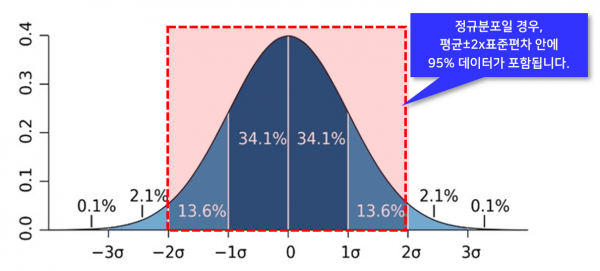
데이터가 정규분포를 가질 경우, 평균±2x표준편차 범위에 95%의 데이터가 포함됩니다. 따라서, 실무에서 표준편차는 '데이터가 정규분포를 가질 경우, 95%에 해당하는 대부분의 데이터는 평균±2x표준편차 안에 들어간다' 라고 해석할 때 주로 사용됩니다.
표준편차로 대부분의 데이터가 포함되는 범위인 '평균±2x표준편차'를 설명하려면, 해당 데이터 집단은 반드시 정규분포를 가져야 합니다.
하지만 실무에서 다루는 데이터는 일부 정규분포를 갖는 경우도 있지만, 완벽한 정규분포를 갖는 데이터는 없으므로 보통 '왜도'와 '첨도'를 바탕으로 데이터의 정규분포 여부를 대략적으로 판단합니다. 실무에서 왜도와 첨도로 정규분포를 판단하는 기준은 아래와 같습니다.
-2 < 왜도 < 2
-3 < 첨도 < 8
일 경우, 정규분포를 갖는다고 해석합니다.오빠두Tip : 정규분포일 경우 "왜도=0, 첨도=3"이 됩니다.실전 예제를 통해 데이터 집단의 통계지표를 구하고, 주어진 통계지표를 바탕으로 데이터 분포를 예측해보겠습니다.
- 통계지표 구하기 : 예제파일을 실행한 뒤, [데이터 안정성] 시트로 이동합니다. 이후 P2셀에 아래 수식을 입력하여 데이터 집단의 표준편차를 구합니다. STDEV.S 함수에 대한 자세한 설명은 아래 관련포스트를 참고하세요.
=STDEV.S(M3:M4736)
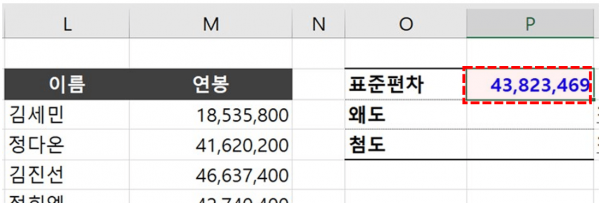
STDEV.S 함수로 표준편차를 계산합니다. 오빠두Tip : 엑셀 STDEV.S 함수 상세설명 및 주의사항 바로가기 - P3셀에 아래 수식을 입력하면 왜도가 계산됩니다. SKEW 함수에 대한 자세한 설명은 아래 관련 포스트를 참고하세요.
=SKEW(M3:M4736)
SKEW 함수로 왜도를 계산합니다. 오빠두Tip : 엑셀 SKEW 함수 상세설명 및 주의사항 바로가기 - P4셀에 아래 수식을 입력하면 첨도가 계산됩니다. KURT 함수에 대한 자세한 설명은 아래 관련 포스트를 참고하세요.
=KURT(M3:M4736)
KURT 함수로 첨도를 계산합니다. 오빠두Tip : 엑셀 KURT 함수 상세설명 및 주의사항 바로가기 - 각 표준편차와 왜도, 첨도를 계산했습니다. 왜도와 첨도가 모두 매우 큰 값을 가지므로, 데이터 분포는 '왼쪽으로 뾰족한 형태'를 가질 것이라고 예측할 수 있습니다.
- 히스토그램 만들기 : 예제파일의 I2:J38 범위에 히스토그램을 만들기 위한 도수분포표를 미리 작성해드렸습니다. 히스토그램을 빠르게 만드는 방법은 이후 강의로 준비해드릴 예정입니다. 예제파일의 I2:J38 범위를 선택한 뒤, [삽입] - [추천차트] 로 이동합니다. 이후 세로막대형 차트를 삽입합니다.
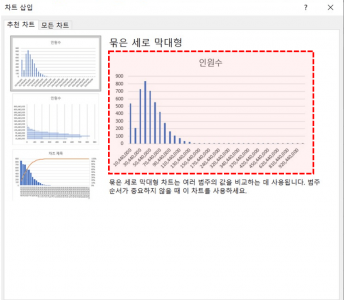
도수분포표 범위를 선택한 뒤, 삽입 - 추천차트에서 세로막대형 차트를 삽입합니다. - 차트의 제목과 눈금선을 지운 뒤, 막대를 우클릭 - 데이터계열서식으로 이동합니다. 이후 간격 너비를 0%로 변경하면 히스토그램이 완성됩니다. 통계지표로 분석한 것과 같이, 데이터가 왼쪽으로 뾰족한 형태로 분포하는 것을 확인할 수 있습니다.
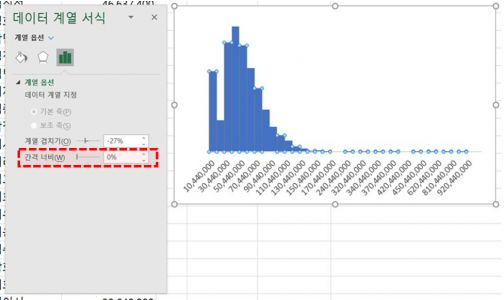
막대 간격너비를 조절하면 히스토그램이 완성됩니다.



